贝塞尔曲线于1962,由法国工程师皮埃尔·贝塞尔(Pierre Bézier)所广泛发表,他运用贝塞尔曲线来为汽车的主体进行设计。贝塞尔曲线最初由Paul de Casteljau于1959年运用de Casteljau算法开发,以稳定数值的方法求出贝兹曲线。贝塞尔曲线不仅仅可以应用到工业设计中,在计算机动画开发中同样占有一席之地,通过构造贝塞尔曲线模拟物体运动的轨迹、速度甚至加速度,来达到想要的动画效果。在CSS开发中使用‘cubic-bezier’方法,传递三次贝赛尔曲线的两个控制点P1和P2来生成一条平滑的曲线。甚至也有很多javaScript动画库使用贝赛尔曲线来实现完美的动画效果。
一、简介
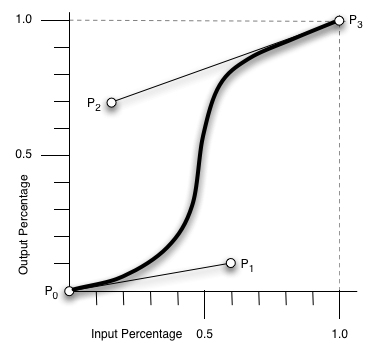
而我要做的通过贝塞尔曲线的原理生成Android动画插值器,在Android平台上实现基于贝赛尔曲线的动画效果。想要了解Android动画原理请先阅读这篇文章。了解贝塞尔曲线绘制过程可以先阅读贝塞尔曲线扫盲,写的很好。
二、De Casteljau算法
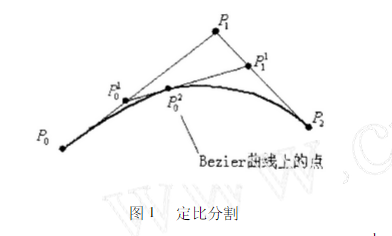
贝塞尔曲线常见的算法是可以通过多项式、De Casteljau算法和递归算法来进行计算。针对De算法,设P0,P1,P2确定了一条二次贝塞尔曲线q,引入参数t,令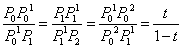 即有:
即有:
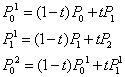
当t从0变到1,第一、二式是两条一次Bezier曲线。将一、二式代入第三式得到:
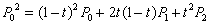
当t从0变到1时,它表示了由P0、P1、P2三个控制点形成一条二次Bezier曲线。并且这个二次Bezier曲线可以分别由前两个顶点(P0,P1)和后两个顶点(P1,P2)决定的一次Bezier曲线的线性组合。以此类推,由四个控制点定义的三次Bezier曲线可被定义为分别由(P0,P1,P2)和(P1,P2,P3)确定的两条二次Bezier曲线的线性组合,由(n+1)个控制点定义的n次Bezier曲线可被定义为分别由前后n个控制点定义的两条(n-1)次Bezier曲线的线性组合:
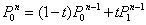
由此得到Bezier曲线的递推计算公式:
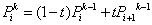
这就是De Casteljau算法。使用这个递推公式,在给定参数下,求Bezier曲线上一点P(t)非常有效。
三、Bezier动画插值器实现
基于De Casteljau算法的递推公式求曲线上点的坐标:
public static Point deCasteljau(Point[] points, float t) {
final int n = points.length;
for (int i = 1; i <= n; i++)
for (int j = 0; j < n - i; j++) {
points[j].x = (1 - t) * points[j].x + t * points[j + 1].x;
points[j].y = (1 - t) * points[j].y + t * points[j + 1].y;
}
return points[0];
}
De Casteljau算法目的是求得曲线上的每一个点,如何用这些采样点描述一条曲线插值器还需要进一步的处理。主要就是处理精度的问题,用距离很近的两个点连线的线段近似描述曲线,理论上采样点越密集描述的越准确,但是很明显在实际项目中不能选择太多的采样点,因为要考虑内存和效率的问题。所以用尽可能少的点尽可能精细的用直线段描述一条曲线,一个不错的做法就是在采样点的在横坐标方向上不要等距分布,而是在曲线变化较快的地方(即斜率较大)采样点尽可能的密集,而在曲线变化平缓的地方采样点选择稀疏。所以需要在通过De Casteljau算法获取初步的采样点后,再进一步获取非均匀分布的采样点,更加处理后的采样点再进行计算。
考虑到针对不同动画的编辑,可能不仅仅是动画进度的插值,还需要动画速度的插值和动画变化率的插值,针对不同曲线类型的变化,通过下面的方式进行扩展。详细代码可以查看这里
四、使用范例
通过控制点构造贝塞尔曲线插值器,例如,可以通过构造一个特殊的插值器,控制drawable的重绘和每个小球的动画并重绘drawable就可以实现类似window phone上经典的Balls Line进度条效果,详细实现可以参考这里。
通过两个控制点构造三次贝赛尔插值器(默认会增加(0,0)和(1,1)作为控制点)。
if (mBezierInterpolator == null) {
// 贝塞尔插值器
mBezierInterpolator = new BezierInterpolator(0.03f, 0.615f, 0.995f, 0.415f);
}
if (mLinearInterpolator == null){
// 普通线性插值器
mLinearInterpolator = new LinearInterpolator();
}
同样可以传递包含所有控制点的List构造插值器。
mBezierInterpolator = new BezierInterpolator(new ArrayList<Point>());
针对BezierInterpolator的构造会有一定的耗时,所以并不建议在需要用到的时候才去构造,也不建议频繁的构造相同的插值器实例。
五、参考文档
3D计算机图形学 Samuel R.Buss
Bezier曲线的算法描述及其程序实现
在线贝塞尔曲线编辑器
window phone loading animation
六、Github
https://github.com/Ivonhoe/BezierInterpolator


